
Introduction 
Introduction 
Introduction And Einstein?
|

So you're the kind of person that wants some evidence--something to support our claim. Well, we've got it for you.
On this page we work with Einstein's most famous equation to illustrate a theoretical prediction of anti-matter. We would like to note that it is uncertain whether Einstein associated what we are about to show you with the existing theories of anti-matter or not. This page is extremely heavy in the math department. However, we try to make this as understandable as possible. There are a few concepts we use that are probably new to the majority of people, so we offer links to pup-up windows that elaborate upon the idea. Ok then, without further delay…
You are probably familiar with:
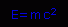 but did you know that that is NOT the entire batch of biscuits (so to speak). In fact, the entire equation is: 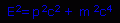 where E is energy, p is momentum, m is mass, and c is the speed of light-usually considered a constant. We will elaborate upon the differences of these equations later. For now, just trust us. Ready to derive? Good!
1: To get rid of the Energy squared (E^2) bit, we must take the square root of both sides. The properties of the square root allow for the extermination of the second power on the E.
 2: Now we are going to rescue a mass * speed of light squared (m * c^2) from underneath the radical and place it outside. But first, we must multiply momentum squared * speed of light squared (p^2 * c^2) by mass squared * speed of light squared over mass squared * speed of light squared (m^2 * c^2)/(m^2 * c^2). Confused? Look at the math below and read this again, that should clear things up.
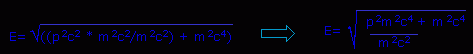
3: Now, to rescue the mass * speed of light squared (mc^2) from the radical we must have mass squared * speed of light to the fourth (m^2 * c^4). Do you see that anywhere? Why yes--in fact there are two! The one in the original equation and the one we created via the talents of Mr. One-derful. By taking the square root of these two instances of mass squared * speed of light to the fourth (m^2 * c^4) we can save the mass * speed of light squared (mc^2).
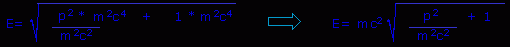 4: Still with us I see, good for you! The speed of light is approximately 299,790,000 meters per second. For the purpose of this page, let's assume the medium through which light is traveling remains the same. Thus, the speed of light can be considered constant. Substituting that speed value in for c, we notice that the denominator in the only term with variables becomes huge. As we multiply c by any given mass, the denominator becomes even bigger. Essentially, the entire term of momentum squared over mass squared * speed of light squared (p^2 / (m^2 * c^2)) is becoming increasingly tiny. Thus, we can simply delete the radical all together as long as we stick a 2 in the denominator of the term that becomes ever smaller.

5: Now let's use the distributive property to multiply through by mass * speed of light squared (m * c^2).
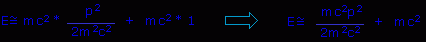 6 (a): Anyone who has taken Physics 101 (a.k.a. Intro to Physics) knows that momentum (p) = mass * velocity (m * v).
6 (b): Keeping that in mind, let's substitute mass * velocity (m * v) in the place of momentum (p).
 7: And a little cancellation...

Here we are. We now have:
 Einstein said the equation of motion is actually E = sqrt(p^2 * c^2 + m^2 * c^4), and that for small momenta (like momenta that we are used to in the everyday world), we can approximate this equation as E = (1/2)mv^2 + mc^2. I bet your thinking what in the world does this have to do with anything. You recognize the second part--the mass * speed of light squared (m * c^2) right? Well first, E = m * c^2 applies only to a particle that is NOT moving. Furthermore, (back to Physics 101) (1/2)mv^2 is the formula for kinetic energy. Thus, the extended Einstein formula (1/2)mv^2 + (m * c^2) applies to a particle that IS moving. So then, what is so important? I don't get it? Well, let's just examine the NON-moving version of the equation (though what we are about to say applies to the moving version as well). Go back to step one--there is a crucial thing we intentionally left out. Go back and look. Did you see it? One of the effects of a taking a square root is that there is a negative and positive answer.
Check this out:
 So then, there are actually 2 variations to Einstein's equation.
 When you substitute any given mass in for a stationary particle in for m and multiply by 8.987*10^16 (c^2 you get a negative and positive answer. The positive answer is the energy that we all deal with everyday. And Negative Energy? Negative Energy--it represents anti-matter! Anti-matter! Holly mackerel! Even Einstein's work seems to confirm the theories of anti-matter. However, it is important to keep in mind that Negative Energy only represents anti-matter--anti-matter does not necessarily have a negative energy level, etc. Remember it is all "relative". This is simply an example of particle symmetry.
|





